What are Foundation Math Questions?
Foundation math questions are based on the essential knowledge that you need in math to be able to complete everyday calculations.
Typical foundation math concepts might include:
- Numbers and number systems (natural numbers, integers, rational numbers, real numbers)
- Basic arithmetic operations (addition, subtraction, multiplication, division)
- Order of operations
- Exponents and roots
- Fractions, decimals, and percentages
- Ratios and proportions
- Algebraic expressions and equations
- Graphing and analyzing functions
- Basic geometry concepts (points, lines, angles, triangles, circles)
- Measurement (length, area, volume, mass, time)
- Probability and statistics (basic concepts and applications)
- Basic financial math (interest, discount, taxes, budgeting, etc.)
Importance of Foundation Math Skills in the Workplace
Generally, foundation math knowledge is required in most jobs - but even more so in roles where you will be working with numbers daily such as accounting, analytics, and engineering.
Knowing how to solve math problems indicates that you have a good logical thinking process and that you can think critically to solve problems.
Nowadays, many employers use aptitude tests to assess skills like math before hiring employees.
Understanding the foundations of math, and knowing the types of questions that you might face in a job test will help you perform well in your potential employer assessments when applying to roles.
Types of Job Tests with Math Questions
There are several types of job tests that you might face when you are applying for a new role, and some of these will have math questions.
You might face the following types of tests:
- Foundation math skills test
- Numeracy tests
- Financial reasoning tests
- Numerical reasoning tests
- Diagrammatic reasoning tests
The above tests will contain basic problem-solving skills using math concepts.
While the numeracy and basic math skills tests will have simple math problems to solve, the numerical reasoning test requires you to interpret and understand data in a table or graph, and then answer a related question on that data. The answer to the question can be found by completing some form of calculation using the data presented.
Foundation Math Questions That You Might Get Asked On A Job Test
Basic math skills test example question
Complete the below sequence of numbers:
2, 3, 5, 7, 11, 13, __
- 15
- 17
- 19
- 16
The answer is b) 17 - the sequence is the first six prime numbers, so the next number would be 17.
Numeracy test example question
What is the median number in the group of numbers below?
15, 19, 13, 14, 18, 12, 20, 16
- 13
- 14
- 15
- 16
The answer is d) 16 - to find the median, you need to put the numbers in numerical order to find the number that is in the middle. This would then look like 12, 13, 14, 15, 16, 17, 18, 19, 20. You can then see that the middle number is 16.
For more numeracy and basic math questions, you can get practice tests here.
Numerical reasoning test example question
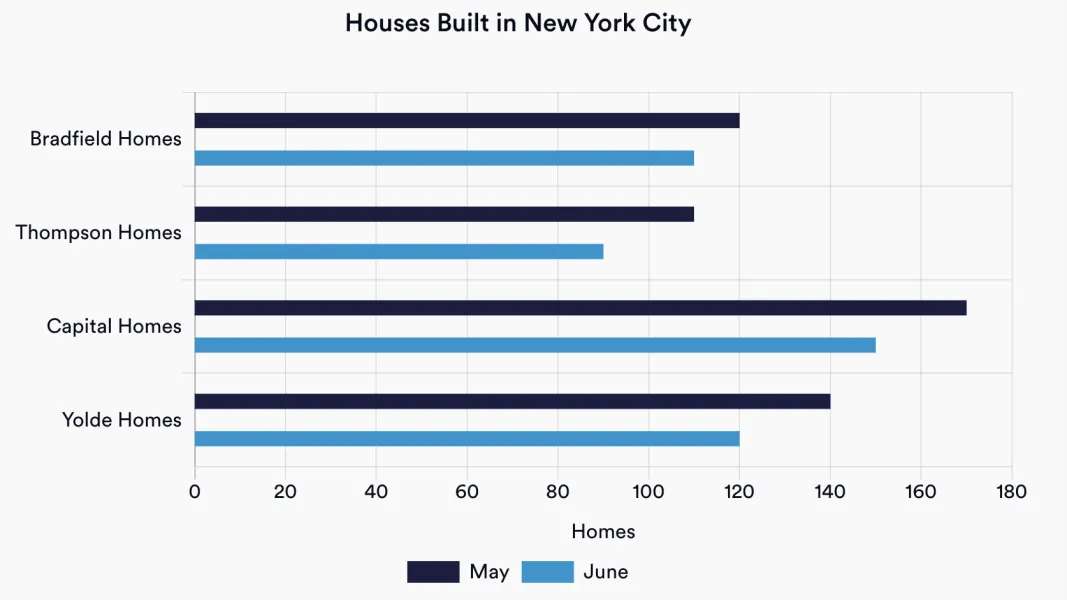
According to the table, by how much did the number of properties built decrease from May to June?
- 120
- 170
- 50
- 70
The table shows that there were a total of 540 homes built in May, and 470 in June.
Answering this question requires just a simple subtraction, but the difficulty can arise when the numbers on the bottom axis are not always clear - you need to be able to judge where the bars end when they are between the given scales.
You can find more numerical reasoning questions and more information about these types of tests here.
Basic Arithmetic Operations
Basic arithmetic operations are the bread and butter of math questions, and you will often need to use these as well as other calculations to find answers.
Remember that in some tests you will be allowed to use a calculator, while in others you won’t - so you need to be confident in finding your answers in both ways.
Addition and Subtraction
Addition and subtraction questions might be single or multiple-digit calculations, but they can also include things like decimals, percentages, and fractions - so you need to have strategies in mind to deal with these.
In most cases, even if you are not permitted to use a calculator, you will be able to use scrap paper and a pen to help you, if you need it.
Multiplication and Division
Multiplication and division questions can often catch you out, and when they come up on non-calculator tests you will need to have a reliable strategy that you fall back on - especially
when it comes to working under pressure.
The questions are usually built to be easily solvable without a calculator.
Order of Operations (PEMDAS/BODMAS)
When dealing with a complex equation or expression, the right answer can only be found if you complete each part of the calculation in the right order, and that is where PEMDAS or BODMAS will help.
Parenthesis, Exponents, Multiplication, Division, Addition, and Subtraction for US candidates, while UK students will have learned Brackets, Orders, Division, Multiplication, Addition, and Subtraction.
This acronym will help you approach the calculation properly so that you can find the right answer.
Fractions, Decimals, and Percentages
Fractions, decimals, and percentages are often used in math questions because they can be converted into each other, and they can be used for everything from price reductions and taxation additions in retail all the way through to calculating increased profits in a ledger.
Simplifying and Comparing Fractions
Fractions are used to describe the parts of a whole, and they are much easier to deal with when they are simplified. This means having them as the lowest possible numbers.
To simplify a fraction, you need to be able to divide the numerator (the number on top of the fraction) and the denominator (the number at the bottom of the fraction) by the highest common factor.
A simple way to see how this works is to look at the fraction 12/16. Both of these numbers can be divided by 4, which is the highest common factor, making the simplified fraction ¾.
To compare fractions, they need to have the same denominator. This means that you need to multiply them by whatever number will work to get the denominators as the same number
So, if we needed to work out which was bigger, 12/16 or 30/32, we need to make sure that they have the same denominator. In this example, we need to multiply the first fraction by 2 (and both the numerator and the denominator should be treated the same) so we get 24/32 and 30/32, so we can see that the second fraction is larger.
Converting Between Fractions, Decimals, and Percentages
To convert a decimal to a fraction, we need to write it as a fraction with a denominator of 100, then simplify. So, 0.75 would become 75/100, which simplifies to ¾.
To convert a fraction to a decimal, it is easier if you can make it have a denominator that is a multiple of 10 - so, ½ becomes 5/10 which we know is 0.5 (five-tenths). If you cannot make it a multiple of ten, then you can simply divide the numerator by the denominator.
To convert a fraction to a percentage, you can either make the denominator 100 (which is the easiest way), so ¾ becomes 75/100 and then we know that is 75%, or you can convert it to a decimal first. All you need to do once you have the decimal is multiply it by 100.
To convert a percentage into a decimal or a fraction, just divide it by 100. 25% then becomes 0.25, or 25/100 which simplifies to ¼.
Percentage Increase and Decrease
There are two main ways to work out the percentage increase or decrease.
Firstly, you can calculate the amount of the percentage increase or decrease, then add or subtract it from the given amount.
For example, a 10% increase of $50 would be $5, so you would add $5 + $50 and get $55.
A 10% decrease would end with the calculation $50-$5, making the answer $45.
You can also add or subtract the percentage from the original amount and make it a decimal, then multiply by that number.
For example, 100% +10% = 110%, which as a decimal would be 1.1. $50 x 1.1 = $55.
100%-10% = 90%, which as a decimal would be 0.9. $50 x 0.9 = $45.
Ratios and Proportions
Ratios are really important when it comes to comparing the amounts of things relative to each other, and they can be used for analyzing data but also for creating scale drawings and models, and even reading maps.
Simplifying Ratios
Ratios are presented in the form of x:y, or sometimes a:b:c.
To simplify a ratio you would need to treat them in the same way as a fraction - by dividing each side of the ratio by the highest common factor.
So, a ratio of 16:12 could be simplified as 4:3 (by dividing each side by the highest common factor of 4).
Calculating Proportional Values
To calculate proportion, you will need to know the total amount, and how many portions are needed.
If you were calculating the proportion of sweets that Fred had in comparison to Amy, when there are 50 sweets and the ratio was 3:2, the calculation would be as follows.
Total number of parts 3 + 2 = 5
Total number of sweets divided by the number of parts: 50/5 = 10
Fred gets 30 (10 x 3) and Amy gets 20 (10 x 2)
Solving Problems Involving Ratios and Proportions
When it comes to solving questions that involve ratios, there will often be a word problem used - so one of the most important things you can do is make a note of the numbers and ensure that you have it all in the right order.
In the question above, you might miss that Fred’s name came first, so his proportion is on the left of the colon (:) sign - and that would mean that despite getting the calculation correct, you would have given the wrong proportion as your answer.
Algebra
Algebra equations are where at least one value is unknown - often represented with a letter or symbol.
Below are different types of algebraic questions you might need to know about.
Simplifying Expressions
When you are simplifying an expression, remember that you are just making it easier. This means reducing it down to the most straightforward form that it can be.
To do this, make sure that you are following the order of operations (PEMDAS or BODMAS), and work through it logically.
- Expand the brackets
- Collect like terms
- Rewrite the expression.
So, for the expression 5x+ 4+2(3x+2) the steps would be:
- Expand the brackets: 5x + 4 + 6x + 4
- Collect the like terms: 5x + 6x = 11x, and 4 + 4 = 8
- Rewrite the expression 11x + 8
Solving Linear Equations
An equation is balanced with an equals sign in the middle, so you know that the figures on the left of the equals sign have the same total as the figures on the right.
Solving these equations means working out what the hidden numbers are (those that have been replaced by a letter).
In the equation, whatever you do to one side has to happen to the other as well.
So, for the equation 3x + 8 = 26, to start with you would take 8 away from each side, leaving the equation as 3a = 18. Then you can divide 18 by 3 to find the answer, which is 6.
Balance is key to solving any linear equation.
Word Problems Involving Algebra
Word problems can add a layer of difficulty to algebra because the math can be hidden - but as long as you can isolate the numerical values that you need to work with, it doesn’t have to be that complicated.
Make use of your scrap paper and pen to ensure that you get all the information you need to create the expression or equation.
Data Interpretation and Statistics
Reading and Interpreting Charts and Graphs
Charts and graphs are usually used as the basis for questions in numerical reasoning assessments, and you need to be able to read and understand the data contained in them to be able to get the right answers.
There are different graphical representations of data that you might come across, including:
- Bar graphs
- Histograms
- Line graphs
- Pie charts
- Scatter graphs
All you need to know is that the data will be put into the relevant graph or chart, and there will be a scale and labels included so you can see the information.
Calculating Averages (Mean, Median, and Mode)
Averages can be shown in different ways. The most common is the mean, which is what most people describe as the average.
The mean number in a group of numbers can be found by adding together all the numbers, then dividing that by the number of numbers. For example, the mean of 3,4, and 5 can be found by adding 3+4+5=12 and then dividing it by 3, which is 4.
The median is the middle number when the numbers are put in numerical order. In the above example, the median would also be 4.
The mode is the number that appears most often. It is easier to find the mode when the numbers are put into numerical order.
The range is the difference between the highest and lowest values in the group of numbers. In the above example, the range would be 5-3=2.
Basic Probability Concepts
Probability can be represented as either a decimal between 0 and 1, or a percentage. The number represents the likelihood or chance that a particular event will occur.
A value of 0 or 0% means that there is no chance, while a value of 1 or 100% means it will happen.
56% or 0.56 shows that there are 56 chances out of 100 that the event will occur. If we had a bag of sweets that contained both blue and red sweets, this would make the probability that we would pick a blue sweet at 0.56, and a red sweet at 0.44.
Unconditional probability means that the chance is out of the full total of the sample, while conditional probability uses a specific subset of the total data.
How To Prepare for Foundation Math Questions on Job Tests
1. Assess Your Current Math Skills
Before you begin preparing for any type of math test, you need to know where your current strengths and weaknesses are. You can do this by taking practice tests online - these simulate job tests and they are an excellent way to get to know what you are already capable of. From the results of this test, you will be able to tell where you might need to revise.
2. Use Online Resources and Practice Tests
There are many different types of foundation math questions that are available online - you can find tests from a variety of different publishers that an employer might use to assess your skills as well as example questions.
3. Manage Your Time Effectively
Math questions in job tests are usually timed, so you’ll need to work fast and accurately when you are going through the test. You should find out how long the test you will be taking is, then work out how long you will have for each question. You can then practice problem-solving within this time limit.
4. Double-Check Your Calculations
Be sure that you double-check your answers. Double-checking your answer is a simple way to make sure you have performed your calculations correctly and reduces your chances of errors.