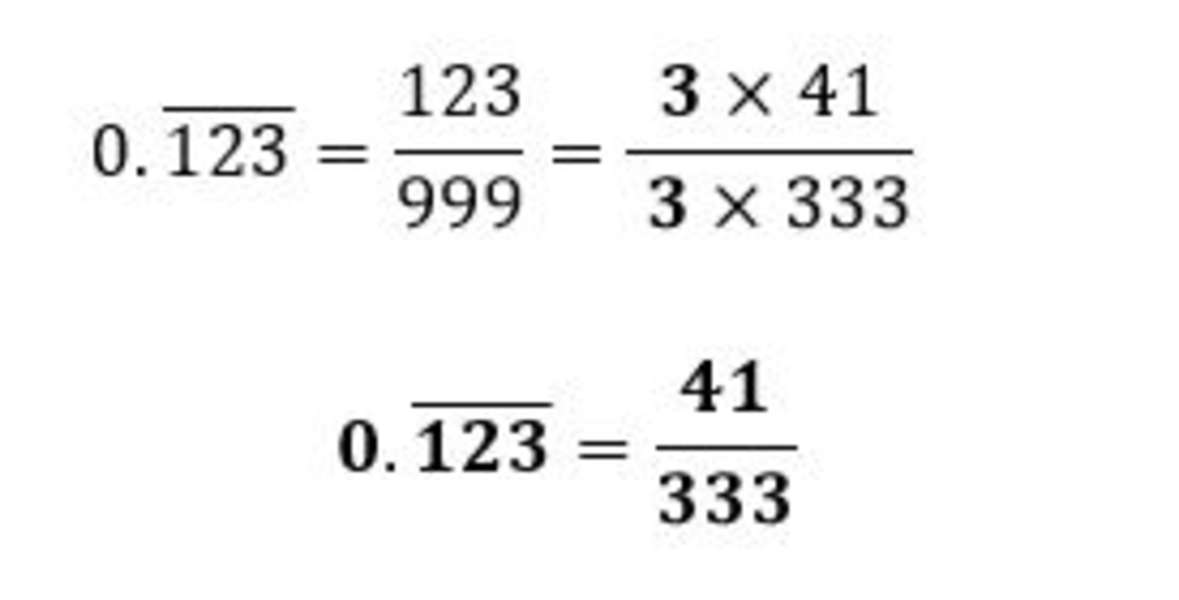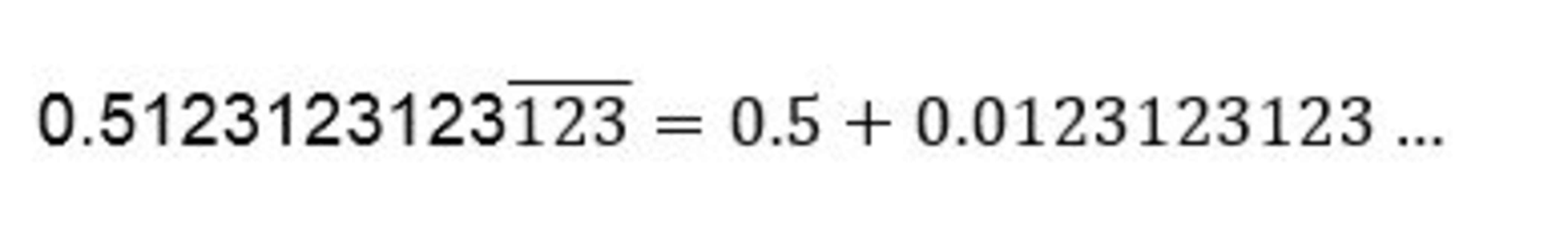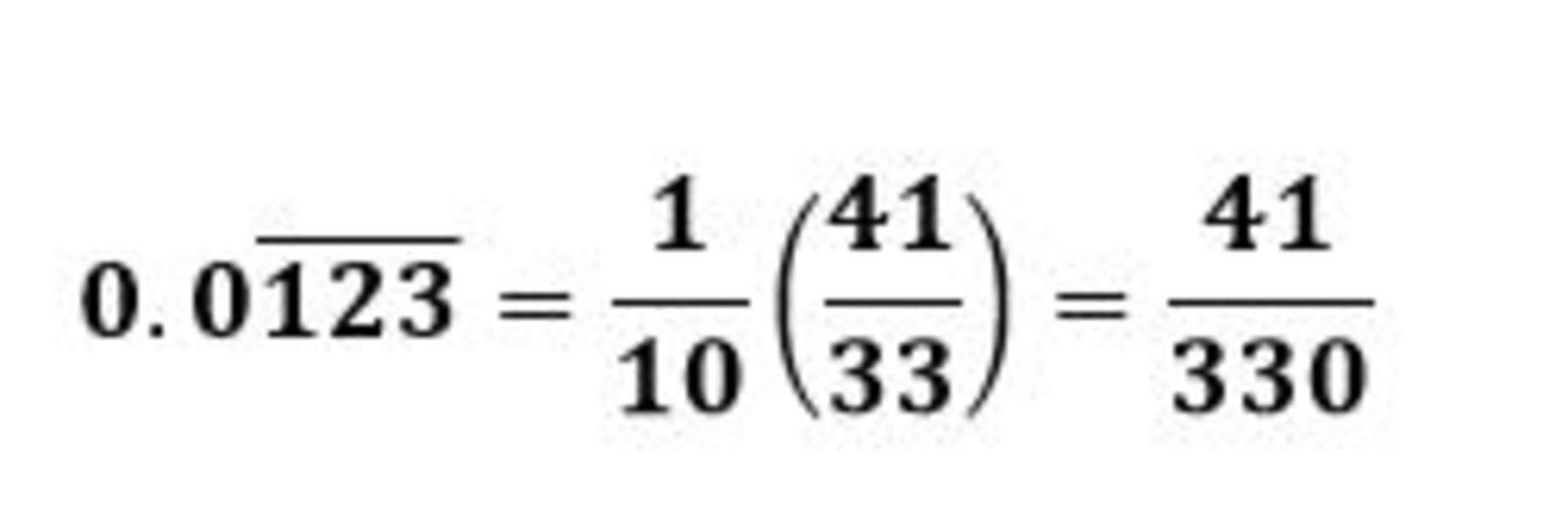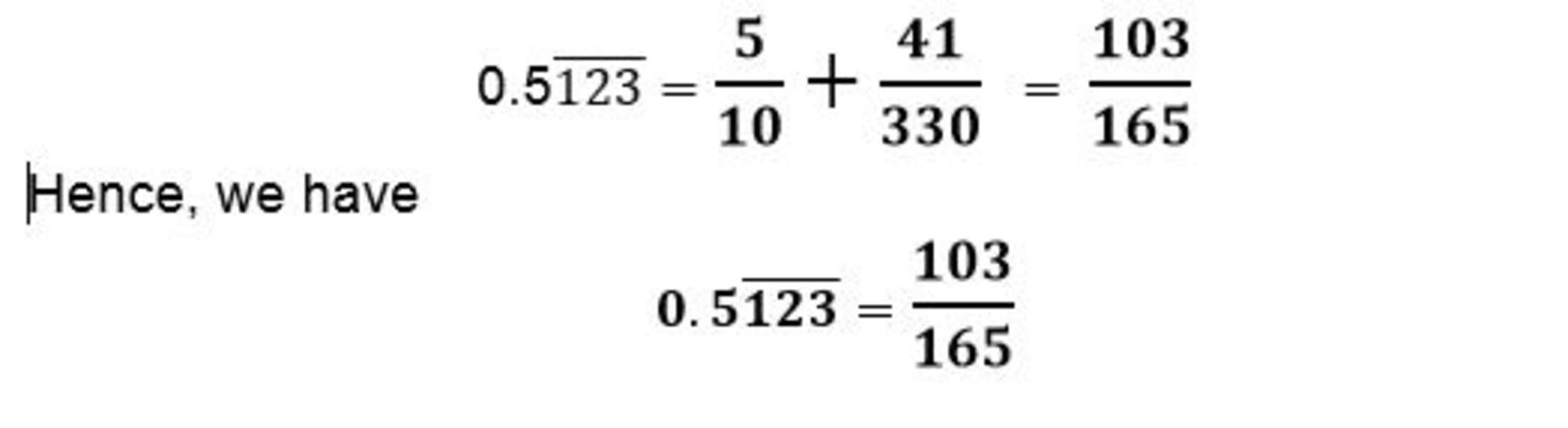Step 1: Count the number of recurring digits
For example, if we want to change 0.567567 to a fraction, there are three recurring digits: 5, 6 and 7.
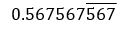
Step 2: Convert to a fraction
We write the first set of the recurring digits as the numerator and the denominator with a series of 9s, depending on the count from Step 1. Since we counted three and we have 567 as the numerator, the denominator would have three 9s.
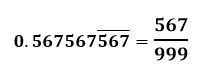
Step 3: Simplify the fraction
Cancel common factors to simplify the fraction.
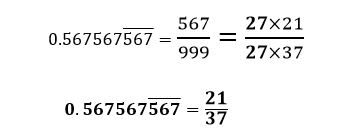
Examples of how to work out recurring decimals
Q) Express the following recurring decimals to fractions.
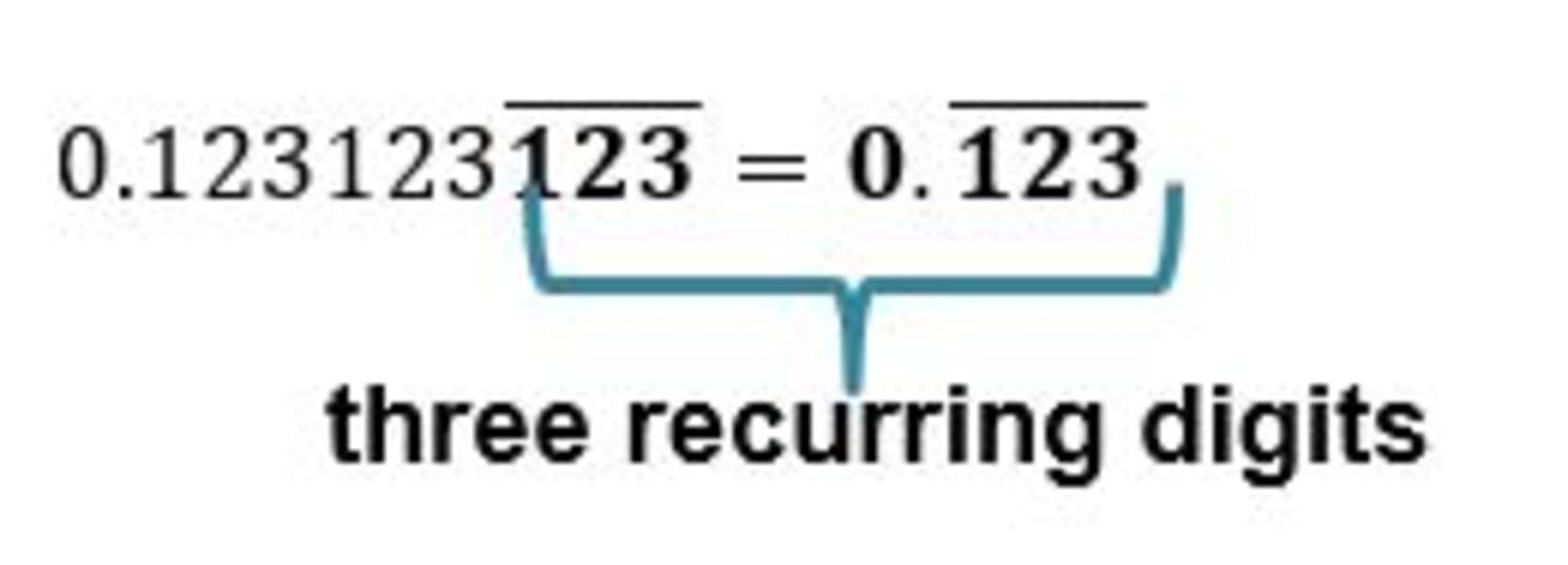
a. To change 0.123123 to a fraction, we first count the number of digits that are recurring.
We would have three 9s on the denominator and 123 as the numerator.
0.(123) ̅=123/999
Look for common factors shared by the numerator and denominator to simplify the fraction.
b. Now to change 0.5123123123, we first separate the recurring and non-recurring digits.
Express 0.5 as a fraction: .5= 5/10.
To express 0.0123123 as a fraction, we can use the value of 123 from part a. So, we have 123 ̅= 123/99=41/33.
Since there’s only 1 zero before the recurring digits, we multiply 41/33 by 1/10.
Now, to find the value of 0.5(123) ̅, we combine the values of the decimals.