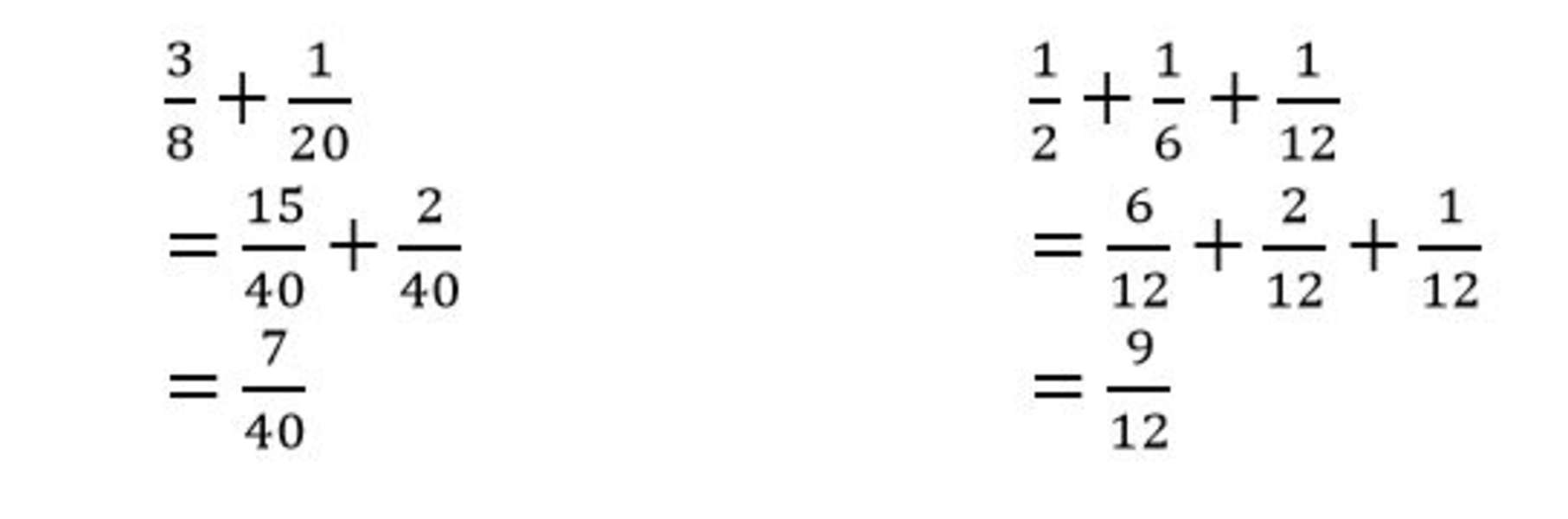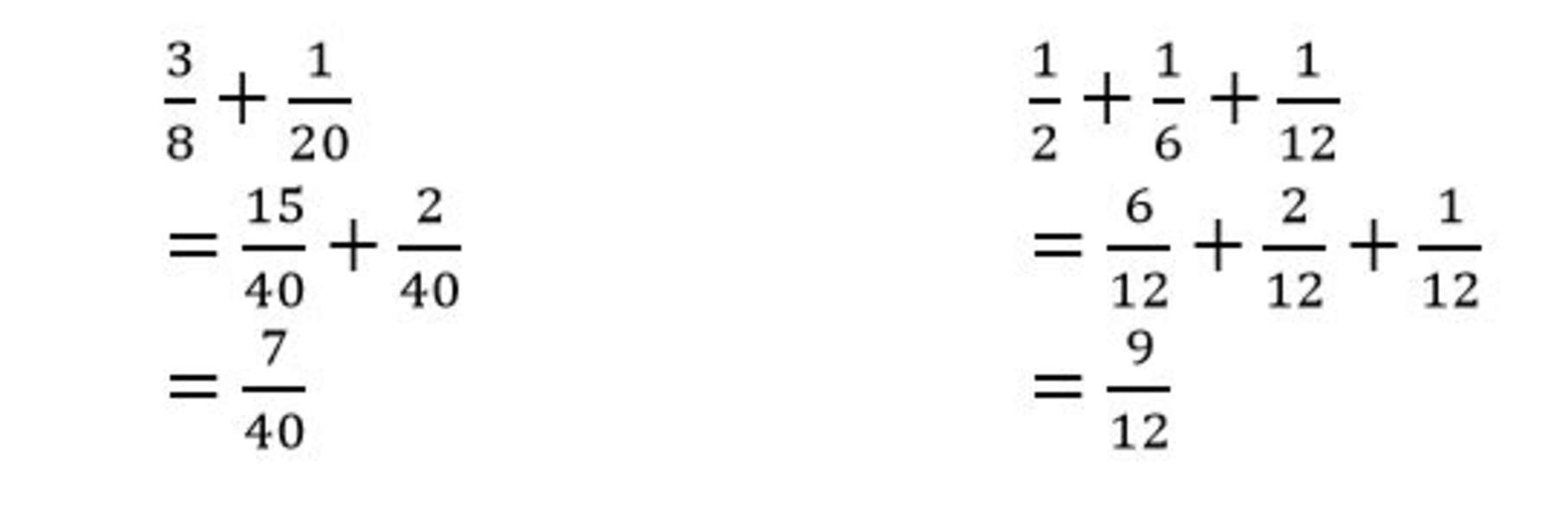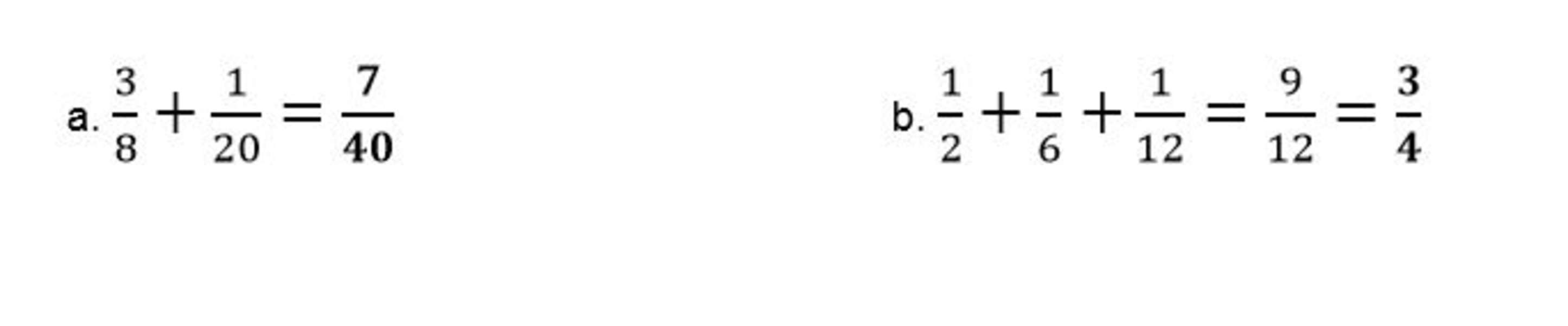Step 1: Check the denominators are different
Confirm the denominators of the fractions are different
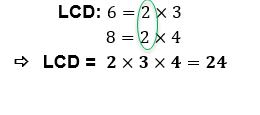
Step 2: Find the least common denominator
Next you need to find the least common denominator (LCD)
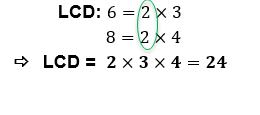
Step 3: Rewrite the fractions so they share the same denominator
Multiply the numerator with the factor needed to come up with the least common denominator.
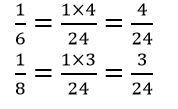
Step 4: Add the numerators
Since the denominator are now alike, add the numerators and write LCD as the denominator to find the sum.

Step 5: Simplify fractions
Simplify the sum if needed.

Examples on adding fractions with different denominators
Q1) Find the sum of the following sets of fractions:
Find the least common denominator shared by the sets of fractions.
Express the fractions so that they share common denominators.
Write the new fractions and find the sum by adding the numerators.
Simplify the sum when needed.