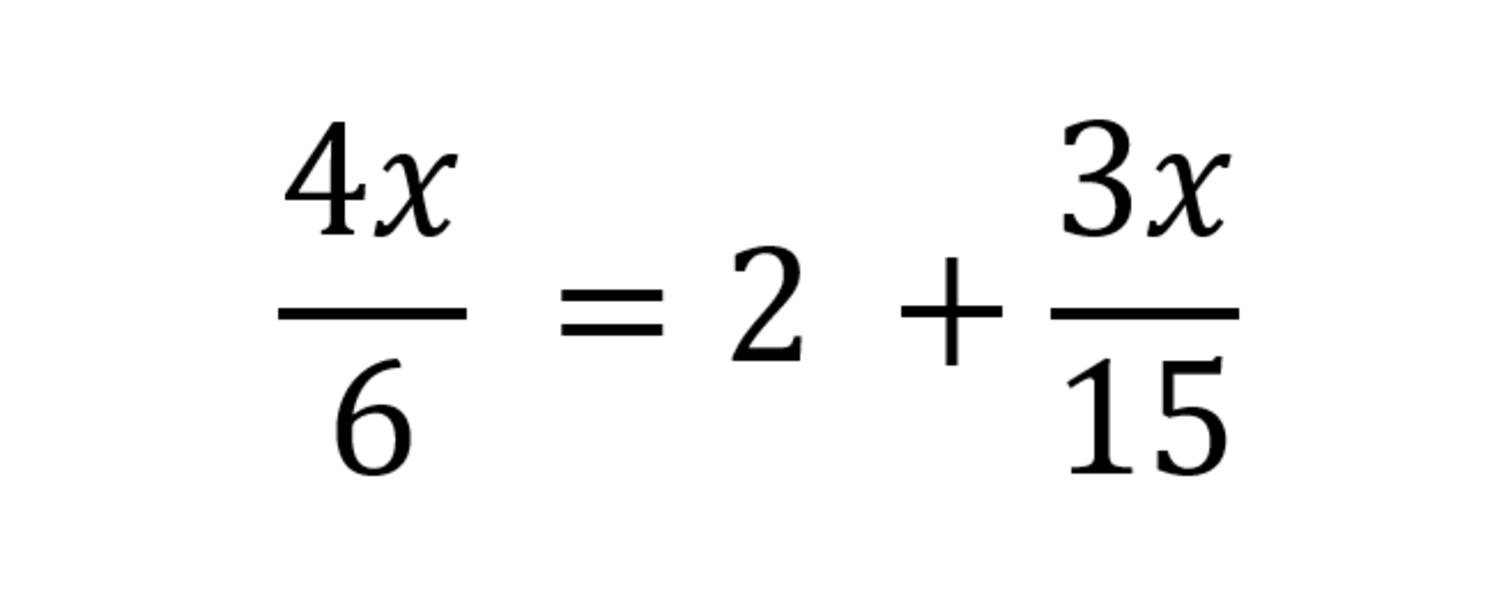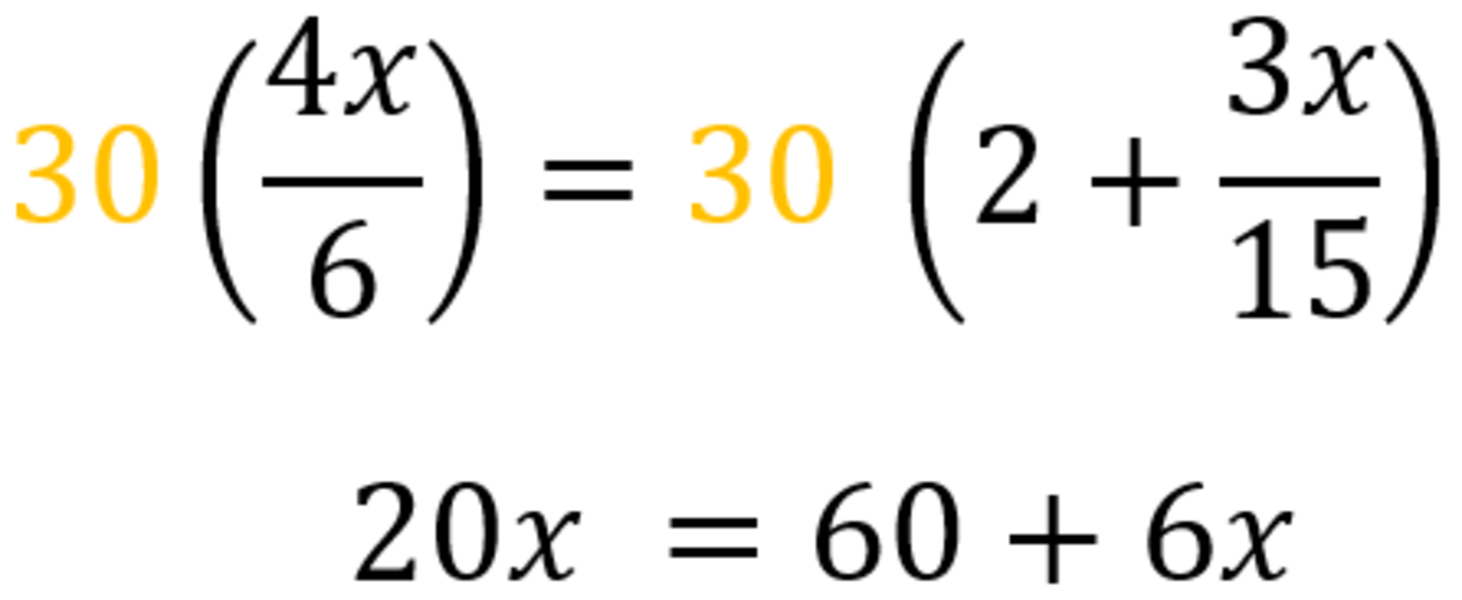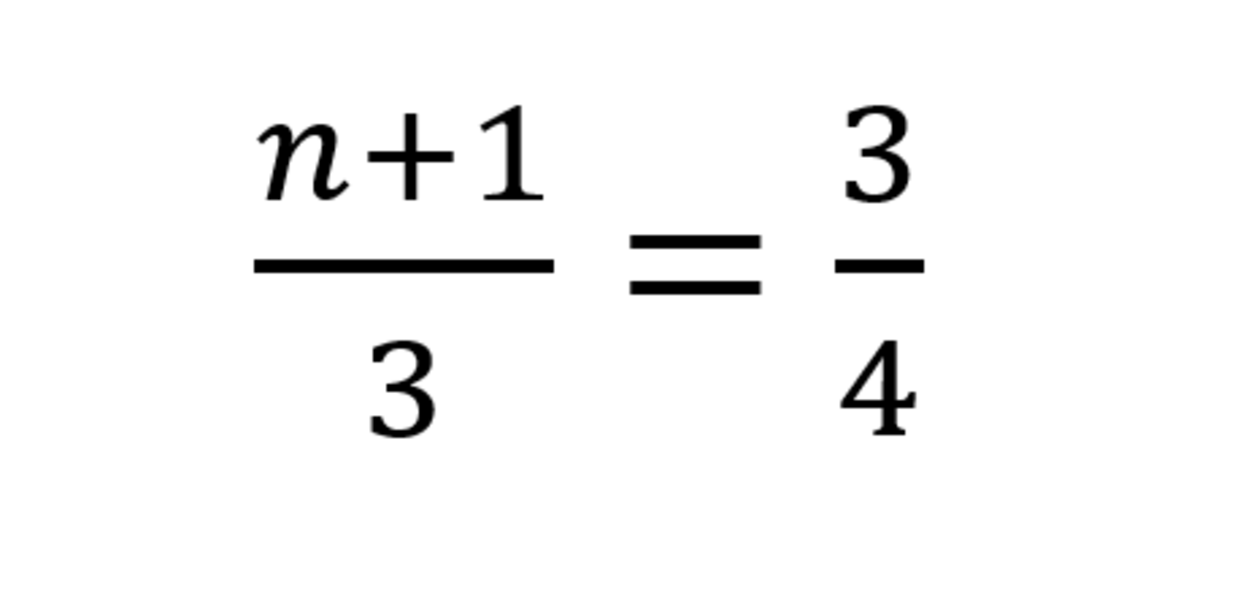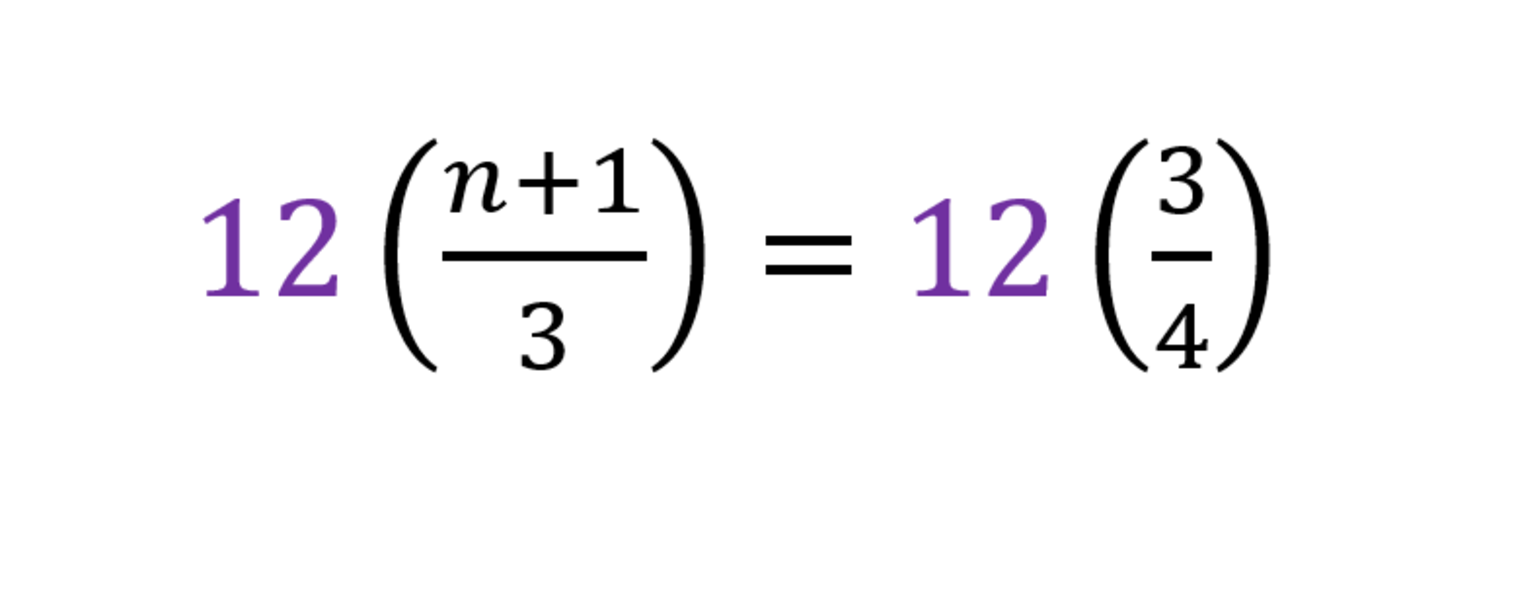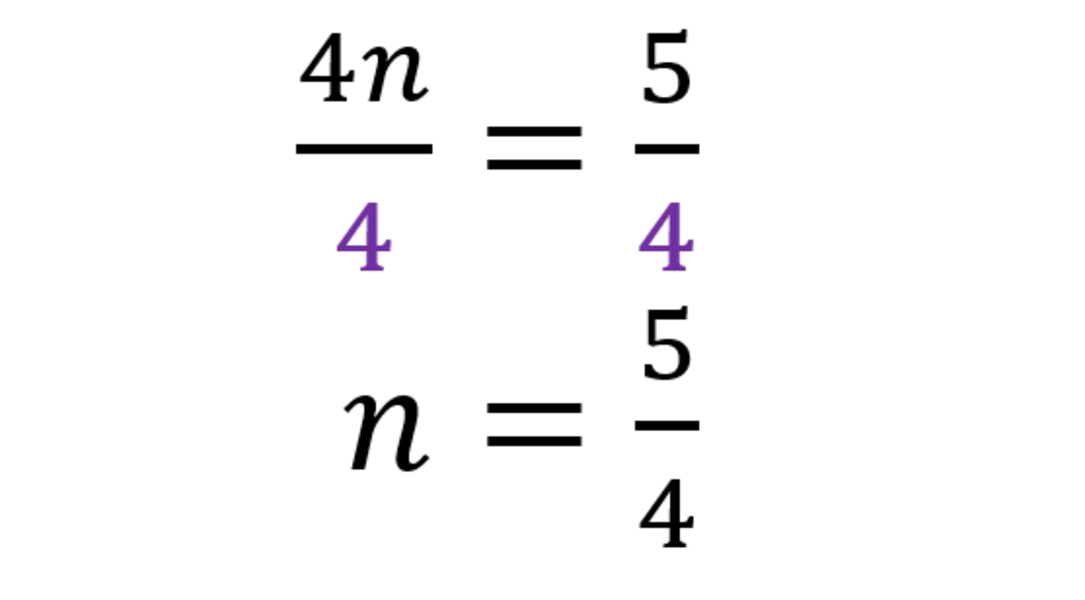What is an equation?
An equation is a statement used in mathematics to show that two items are equal. In fractions, an equation is used to find the value of a fraction when one or more of its parts are unknown.
If you’re stuck on a math problem that involves fractions, don’t worry! In this article, we’ll show you how to solve equations with fractions step by step.
Step 1: Find the least common denominator
Firstly we need to find the least common denominator (LCD) of the fractions found in the equation, which is the smallest number that can be a common denominator for both of the fractions. For this equation the LCD is 12 as this is the lowest common multiple of 4 and 6.
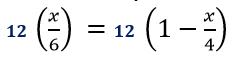
Step 2: Multiply the least common denominator
Multiply the LCD to both sides of the equation.
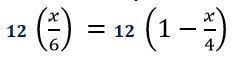
Step 3: Simplify the equation
Simplify both sides of the equation and make sure we’re only working with whole numbers.
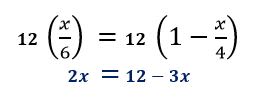
Step 4: Simplify until there's one term on both sides
Move all terms with the variable on one side and further simplify both sides of the Equations so we have one term on both sides.
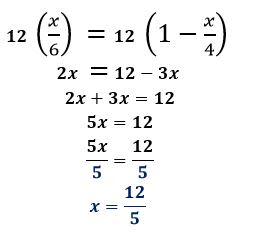
Step 5: Divide the coefficient on both sides
Once the variable is isolated on one side, divide the coefficient on both sides to solve for the unknown variable.
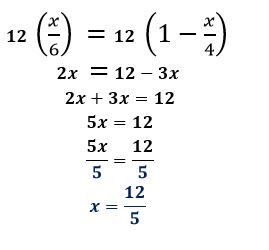
Examples of how to solve equations with fractions
Q1) Find the value of x in:
First, let’s find the least common denominator (LCD) of the fractions:
6=2×3 15=3×5 LCD:2×3×5=30
Multiply 30 on both sides of the equation. Make sure to simplify after distributing 30.
Move 6x on on the left-hand side of the equation to isolate the term with the variable.
20x-6x=60 14x=60
Divide 14 on both sides of the equation to solve for x.
Q2) An unknown fraction is added to 1 and we divide the sum by 3. The result is equal to 3/4. What is the value of the unknown fraction?
We can let n be the unknown number. We can set up the equation to solve the problem.
First, look for the least common denominator (LCD). Since 3 and 4 don’t share any common factors, we find their product.
LCD∶3×4=12
Multiplying 12 to both sides of the equation, we have:
Move 4 on the right-hand side of the equation.
4n=9-4 4n=5
Divide both sides by 4 to isolate n.
Hence, the unknown fraction is equal to 5/4.